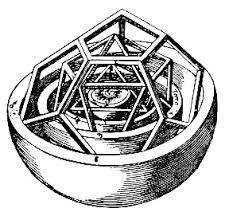
Kepler, in his work Mysterium cosmographicum, published in 1596, had claimed the existence of a relationship between the six planets known at the time (Mercury, Venus, Earth, Mars, Jupiter and Saturn) and the Platonic solids.
As we know, it is to Kepler that we owe the intuition that the orbits of the planets are elliptical: however, at the time of the Mysterium cosmographicum, the German astronomer considered them still circular, in agreement with the opinion of the time. Because of this, the solar system could be represented as a set of concentric circles. A few years before his discovery, Kepler had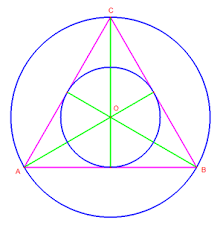 
noticed that, by inscribing an equilateral triangle in a circle, and inscribing in it a smaller circle, the ratio between the radius of the larger circle and that of the smaller circle was equal to the ratio of the orbit of Saturn (major circle) and that of Jupiter (minor circle). It was therefore possible to draw an equilateral triangle between the orbits of these two planets. Broadening the concept, each circular orbit inscribed (and at the same time was circumscribed by) one of the regular polygons (equilateral triangle, square, regular pentagon, etc.), according to a predefined ratio that was supposed to represent the geometric basis of the universe.
Having failed, however, to find a disposition of regular polygons that univocally matched his astronomical observations, Kepler decided to use regular polyhedra (the extension of regular polygons in a three-dimensional space), establishing that each of these could at the same time contain inscribed spherical orbits and be circumscribed by them.
Therefore, if six concentric spheres were built (the six orbits of the known planets) and positioned at intervals corresponding to the relative dimensions of the orbits of the planets (assuming that they rotated around the sun with a circular orbit), each of these could have inscribed in itself the lesser Platonic solid, and be circumscribed by the higher Platonic solid.
The solids were arranged by Kepler in the following order (from the innermost to the outermost): octahedron, icosahedron, dodecahedron, tetrahedron, cube. The geometric concept of the solar system took shape as follows:
- the orbit of the innermost planet (Mercury) and that of Venus contained an octahedron;
- the orbit of Venus and that of the Earth contained an icosahedron;
- the orbit of the Earth and that of Mars contained a dodecahedron;
- the orbit of Mars and that of Jupiter contained a tetrahedron;
- the orbit of Jupiter and that of the outermost planet (Saturn) contained a cube.
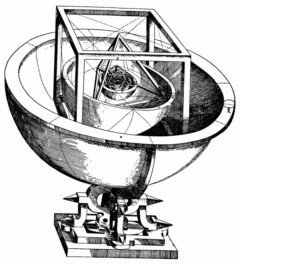
The outer hemisphere represents the orbit of Saturn; the one contained in the cube represents the orbit of Jupiter and the one in the tetrahedron the orbit of Mars, which contains a dodecahedron that encompasses the hemisphere corresponding to the orbit of the Earth. Inside the latter we see an icosahedron, hence the hemisphere corresponding to the orbit of Venus, which contains an octahedron and finally the hemisphere which represents the orbit of Mercury.
The idea of Kepler was abandoned, since not even the use of platonic solids was compatible with astronomical observations, especially after Kepler himself discovered in 1609 that “The orbits of the planets are ellipses, with the Sun at one focus of the ellipse.” (first law of Kepler).
And yet, the Keplerian and Platonic intuition that, at the foundation of every natural and cosmic phenomenon, and therefore also of solar Cycles, there are governing Canons, harmonic or golden rather than arithmetic, responds to the vision of all traditions of the Ancient Wisdom: “God geometrizes” and an Order of Laws or conscious wills guides the evolution of the Whole towards Harmony, the glory of the One.
This article celebrates the today meeting between the solar Mind (Venus, 5th Ray) and the solar Artist (Mercury, 4th Ray) for the second time in the year (the previous one on May 6th).
The substantial waters of Libra welcome this luminous union and respond with as much light (Libra transmits the 3rd Ray): the cosmic Law finds a channel of expression through the two Luminaries and falls to our causal level as an impulse towards proportional relationships and harmonic Forms.
