A point of view is limited in itself.
It gives us a one-way view of the landscape.
Only when multiple complementary views
on the same reality add up one has
full access to the knowledge of things.
The more complex what we want to understand,
the more important it will be to have different pairs of eyes,
so that the beams of light converge
and we can see the One through multiplicity.
This is the the nature of an authentic vision:
putting together already known points of view
and show others hitherto unknown, teaching us that,
in fact, they are all part of the same Whole.
Alexander Grothendieck
We often say that official science is coming to understand and explain what the ancients already knew through intuition or some kind of revelation. This is true, but science has different times and ways of affirming the same truths as the ancients. Its process is much slower and more laborious. A path made up of hard chisel work and small steps one after the other, steps firmly planted on the ground because in order to look at the Uranus Cosmos (the ordered sky of the ancients), it is necessary to have a solid base on which to stand and rely on. [1]
A simple example in order to understand this. We all “intuit” in some way that 1 + 1 = 2. The arithmetic we study at school as children tells us this, but so does our everyday experience, our empirical knowledge. For science, however, “intuition” is not enough, science goes on by “formal demonstrations” and the formal demonstration that 1 + 1 = 2 occupies the first 300 pages of Whitehead and Russell’s Principia Mathematica, a monumental work whose (unsuccessful) aim was to formalise the foundations on which all mathematics is based. Why so much effort to say that 1 + 1 = 2? Because first of all, one has to formally state which actors are involved. What is “1”? What is “2”? What is “+”? And what is “=”? It may seem trivial, but when Whitehead and Russell asked themselves these questions, a chasm of unexpected depth opened up before them, and in order to begin to answer these questions, it was necessary to have a common language with which to define the basic concepts. This common language in which all mathematics can be expressed is the “Set Theory” by Cantor-Frege. Around the middle of the last century, Mac Lane expanded this language by founding the “Category Theory”, which gave much more expressiveness to mathematics and its various disciplines such as geometry, algebra or topology. In the 1960s, Grothendieck further expanded this theory, generalizing it and bringing it to its essence, introducing the concept of “Motive” and “Topos”. But at the beginning, to demonstrate that 1 + 1 = 2 and to answer the not at all trivial questions that we asked ourselves above, Whitehead and Russell used set theory and therefore “1”, in Principia Mathematica, is “the Set of all Sets that contain a single element”. Likewise, “2” is “the Set of all Sets that contain two elements”. “+” becomes an operation of logical union between sets and “=” is a non-trivial concept of equivalence which will reach, with Grothendieck and Morita, its maximum expression of beauty and elegance.

Alexander Grothendieck, who has been called the Albert Einstein of mathematics, used the tool of abstraction to probe the foundations of mathematics ever deeper until he reached its heart. For him, any dilemma could be simplified if it was looked at in its essence. He was not interested in numbers, curves, lines or any other mathematical object in particular, but in the relationship between them. He had an extraordinary sensitivity in finding harmony between things. One of his greatest strokes of genius was to expand the notion of the point. This ceased to be a dimensionless location and came alive with a complex internal structure that contained an infinite universe. All this resulted in the aforementioned concept of Topos. Looking at the world and at reality through the lens of the Topoi is like abstracting ourselves to such an extent that the words of natural language (which we humans invented, while this is not the case for mathematics, as Plato had already intuited) are not enough to describe the experience. It is like observing the “everything” from the perspective of the “not everything”, or the finite from the ‘perspective’ of the non-finite or Infinite, defined in these pages as the “veil of the Absolute”.
These are fascinating and enchanting places of thought, but also extremely dangerous. Grothendieck himself wrote that: “even in mathematics certain things should remain secret forever, for the good of us all”. A statement of this kind may seem exaggerated, but just as in physics there are cosmic monsters such as black holes that literally tear apart space and swallow up anything, even time, in mathematics there are demons that are capable of engulfing and annihilating even thought . Monsters that can drive genius scholars mad, as happened to Gödel (we will discuss this in a moment) or to Grothendieck himself, who wrote: “Humanity lives in the shadow of a new horror”, that of the “sleep of reason” (F. Goya). Yet, beyond the limits of the mind defined as concrete by the esoteric Teachings, other vibrations await to be received by the higher levels of wise intelligence.

Francisco Goya – The Sleep of Reason Produces Monsters
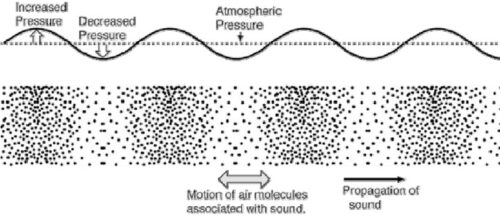
And speaking of “essence”, we must be careful at what level to look for the heart of the phenomena we want to analyse. An example: we often say that Sound and Light have the same essence. But as physical phenomena, the only thing sound and light have in common is that they are two vibrational phenomena. That’s it, the analogies end here.
Sound is the molecular vibration of a physical medium, whether gaseous, liquid or solid; in fact, in empty space (or, according to the Ancient Wisdom, simply more subtle, considering Space as alive or full of Life), outside the atmosphere of the Earth, the deepest silence reigns and is inaudible by ordinary physical means.
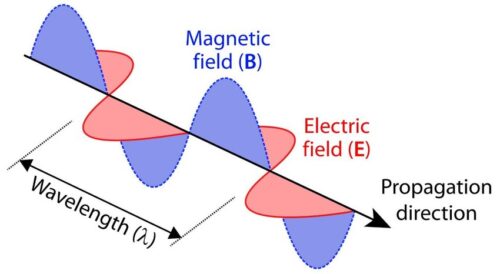
Light is the vibration of something completely different than sound, it is the vibration of a field: the electromagnetic field which can propagate even in the ‘vacuum’ of deep space; and the Universe itself has a vibration of a nature still different from sound and light, its is the vibration of another field: the Higgs Field, responsible for everything that is in manifestation, including the Universe itself which in turn it is a manifest characteristic of the gravitational field. This is to say that stating that sound and light have the same essence presupposes a shared knowledge of the meaning of the word Essence, which is not that of their physical manifestation, where the two entities are not interchangeable. In occult Philosophy, the Ideas of Sound and Light do not therefore mean their phenomenal or physical counterparts, but rather the Vibration of Life at the various levels of spatial Substance.

Kurt Gödel
Like Grothendieck, Kurt Gödel was also interested in the essence, understood as abstract truth or the heart of mathematics and to search for this essence he turned the power of mathematical formalism towards mathematics itself [2]. What he discovered has forever marked the world of logic and mathematics, identifying in its ‘essence’ the same nature of “indeterminacy” [3] that Heisenberg had found in the foundations of Physics a few years earlier. Simply put, what Gödel discovered is that in formal mathematical systems, such as arithmetic, there are statements about numbers that are true, but whose truth cannot be proved using arithmetic itself. Therefore any formal system, for example any numerical system, is by its nature incomplete (this is why Whitehead and Russell’s project failed). It presupposes the intervention of a level of observation or understanding different from that of the intellectual reasoning of mathematical investigation.
Mathematics, maqhmatikóv, as a term, refers to everything related to study, learning and knowledge, but Grothendieck, Gödel and Heisenberg have traced limits beyond which we are not allowed to go with this intellectual knowledge. There are “event horizons” beyond which everything – space, time, thought – lose their meaning. These great thinkers told us that no matter how deep and passionate our study is, there will always be truths that are precluded to us in this manifestation, and science has learnt this since the 1930s. No matter how hard humanity may try, there are barriers, veils, beyond which our physical gaze cannot go. We have to accept this and this applies to any kind of “teaching” learned only through certain levels of the mind. This does not mean, however, that science is limited with respect to intuition or the possibility of developing the tools of perception of everything that “resonates with us in some way”. The cognitive limits are universal or proportional to the various levels of ‘reality’ or consciousness and the sapiential teachings state that: “Humanity will only be able to access certain levels of understanding when it is ready”.
The language that science uses to describe these limits is very complicated, for a few “disciples”, just as the language of esotericism is complicated and is reserved for those dedicated to its study. We all, scientists and esotericists, must strive so that these languages converge more and more and so that scientists do not see esotericists as charlatans and esotericists do not consider scientists blind and deaf. As Grothendieck wrote in the quote at the beginning of this article, only with a common gaze will it be possible to recognize that we are part of the same Whole.
It is important that, for each discipline of study and research, we proceed with an open mind and curiosity, so as to build bridges of thought, connections and therefore common languages that respect the categories of meaning of each “science”, leading to that unification of knowledge and study that, over the centuries, we have forgotten.
___________________________________________________________________
1. What is defined as the “Scientific Method” is based on the observation of the phenomenon, the theorisation of this phenomenon and experimentation to verify the hypothesised theory.
2. This is called a “metamathematical” process.
3. It is impossible to explain here in an exhaustive manner Gödel’s formidable discovery, which are the “Syntactic Incompleteness theorems”. In common language we could summarize his results by saying that any formal system S in which a certain amount of arithmetic can be developed and which satisfies some minimal coherence conditions (there are no contradictions) is incomplete: one can construct an elementary arithmetic statement A such that neither A nor its negation are demonstrable in S. In fact, the sentence thus constructed is then true (in the sense that it is possible) since it expresses its unprovability in S, through a representation in the arithmetic of the syntax of S. Furthermore, one can construct in arithmetic a statement C that expresses the coherence of S, and C is not provable in S if S is coherent.